37 广义可加模型
相比于广义线性模型,广义可加模型可以看作是一种非线性模型,模型中含有非线性的成分。
- 多元适应性(自适应)回归样条 multivariate adaptive regression splines
- Friedman, Jerome H. 1991. Multivariate Adaptive Regression Splines. The Annals of Statistics. 19(1):1–67. https://doi.org/10.1214/aos/1176347963
- earth: Multivariate Adaptive Regression Splines http://www.milbo.users.sonic.net/earth
- Friedman, Jerome H. 2001. Greedy function approximation: A gradient boosting machine. The Annals of Statistics. 29(5):1189–1232. https://doi.org/10.1214/aos/1013203451
- Friedman, Jerome H., Trevor Hastie and Robert Tibshirani. Additive Logistic Regression: A Statistical View of Boosting. The Annals of Statistics. 28(2): 337–374. http://www.jstor.org/stable/2674028
- Flexible Modeling of Alzheimer’s Disease Progression with I-Splines PDF 文档
- Implementation of B-Splines in Stan 网页文档
37.1 案例:模拟摩托车事故
37.1.1 mgcv
MASS 包的 mcycle 数据集
#> 'data.frame': 133 obs. of 2 variables:
#> $ times: num 2.4 2.6 3.2 3.6 4 6.2 6.6 6.8 7.8 8.2 ...
#> $ accel: num 0 -1.3 -2.7 0 -2.7 -2.7 -2.7 -1.3 -2.7 -2.7 ...library(ggplot2)
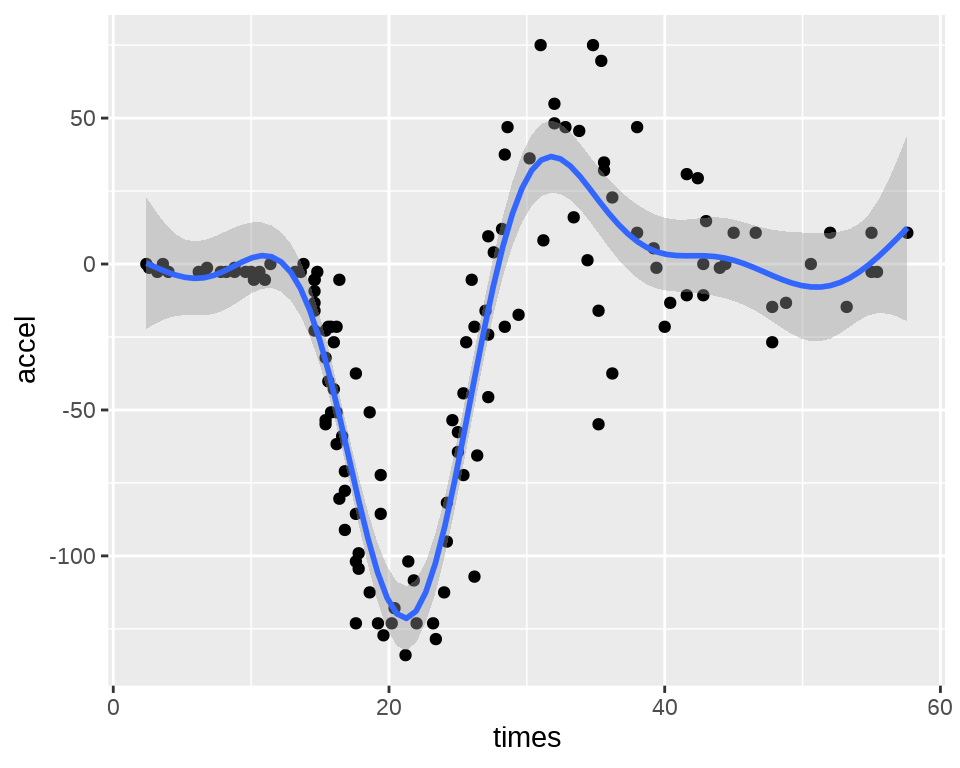
ggplot(data = mcycle, aes(x = times, y = accel)) +
geom_point() +
theme_classic() +
labs(x = "时间(ms)", y = "加速度(g)")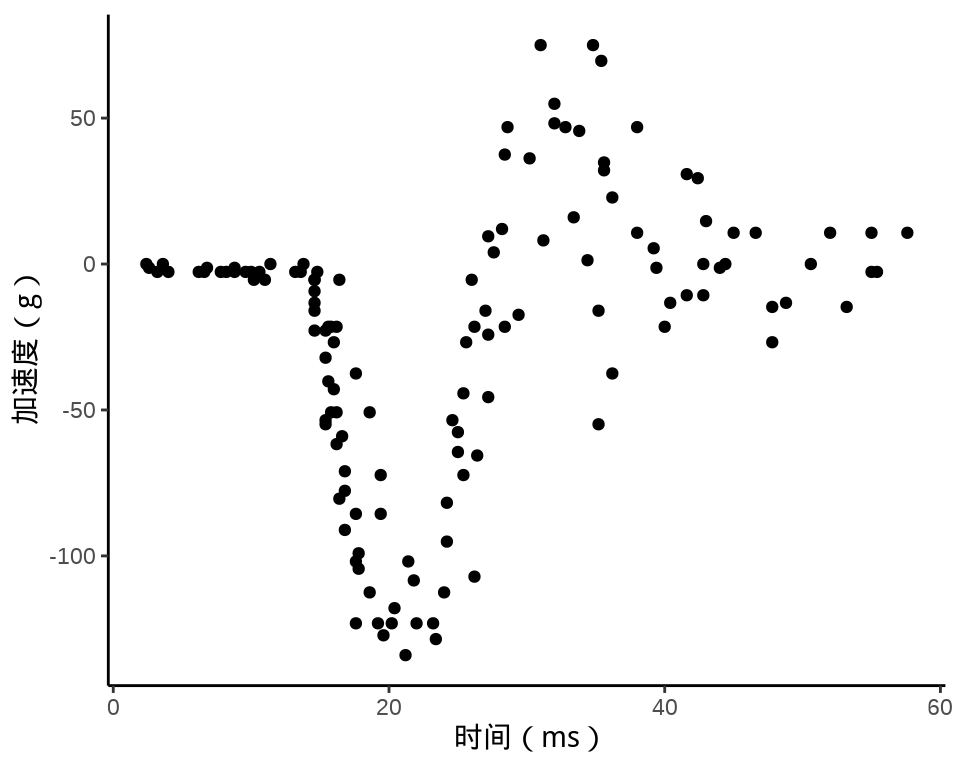
样条回归
library(mgcv)
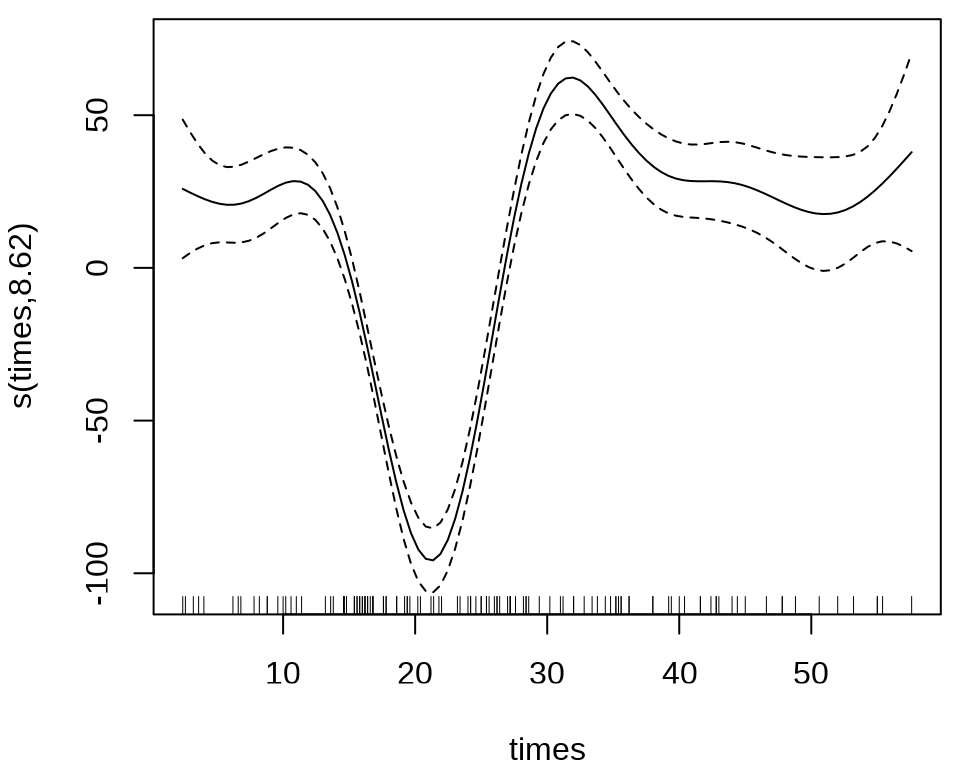
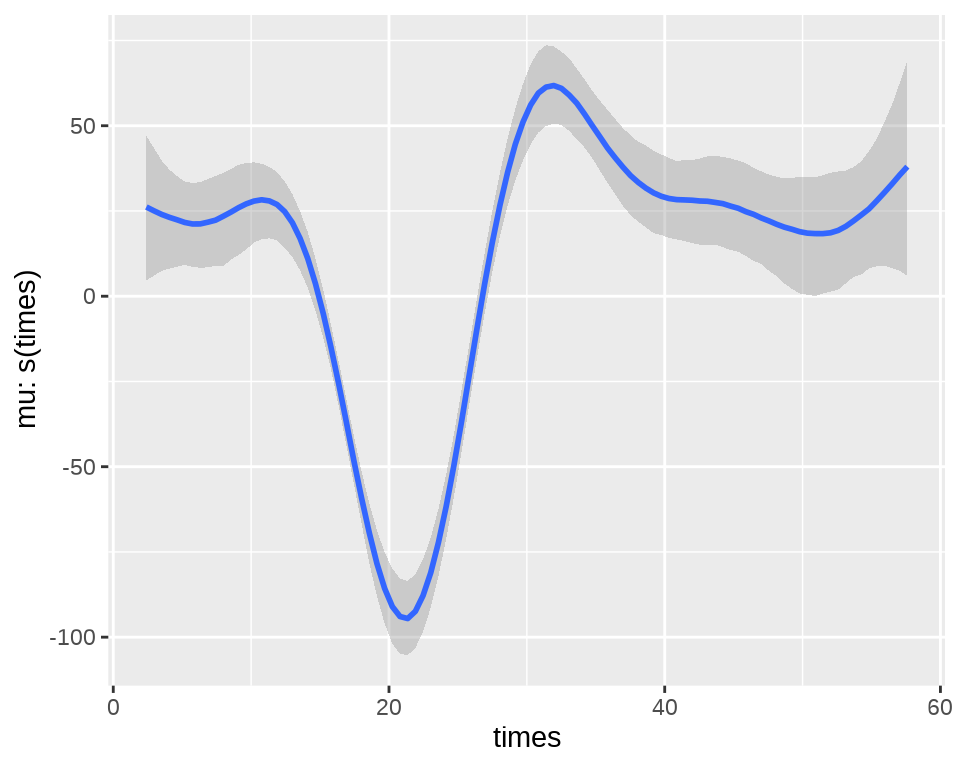
mcycle_mgcv <- gam(accel ~ s(times), data = mcycle, method = "REML")
summary(mcycle_mgcv)#>
#> Family: gaussian
#> Link function: identity
#>
#> Formula:
#> accel ~ s(times)
#>
#> Parametric coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -25.546 1.951 -13.09 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Approximate significance of smooth terms:
#> edf Ref.df F p-value
#> s(times) 8.625 8.958 53.4 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> R-sq.(adj) = 0.783 Deviance explained = 79.7%
#> -REML = 616.14 Scale est. = 506.35 n = 133方差成分
#>
#> Standard deviations and 0.95 confidence intervals:
#>
#> std.dev lower upper
#> s(times) 807.88726 480.66162 1357.88215
#> scale 22.50229 19.85734 25.49954
#>
#> Rank: 2/2ggplot2 包的平滑图层函数 geom_smooth() 集成了 mgcv 包的函数 gam() 的功能。
37.1.2 cmdstanr
37.1.3 rstanarm
rstanarm 可以拟合一般的广义可加(混合)模型。
library(rstanarm)
mcycle_rstanarm <- stan_gamm4(accel ~ s(times),
data = mcycle, family = gaussian(), cores = 2, seed = 20232023,
iter = 4000, warmup = 1000, thin = 10, refresh = 0,
adapt_delta = 0.99
)
summary(mcycle_rstanarm)#>
#> Model Info:
#> function: stan_gamm4
#> family: gaussian [identity]
#> formula: accel ~ s(times)
#> algorithm: sampling
#> sample: 1200 (posterior sample size)
#> priors: see help('prior_summary')
#> observations: 133
#>
#> Estimates:
#> mean sd 10% 50% 90%
#> (Intercept) -25.5 2.2 -28.3 -25.5 -22.8
#> s(times).1 340.7 237.5 33.1 336.2 645.1
#> s(times).2 -1205.4 258.8 -1538.4 -1203.4 -879.0
#> s(times).3 -574.1 153.9 -779.7 -576.7 -377.6
#> s(times).4 -617.8 139.1 -798.1 -618.1 -436.3
#> s(times).5 1060.3 85.3 951.8 1060.3 1166.1
#> s(times).6 -89.4 50.8 -154.7 -88.6 -24.8
#> s(times).7 -233.7 34.5 -277.2 -233.8 -187.9
#> s(times).8 16.1 109.2 -121.5 15.5 153.8
#> s(times).9 -0.2 33.8 -29.6 0.1 27.3
#> sigma 24.8 1.7 22.6 24.8 26.9
#> smooth_sd[s(times)1] 402.7 61.5 325.6 399.3 482.2
#> smooth_sd[s(times)2] 24.2 24.4 2.2 16.6 57.6
#>
#> Fit Diagnostics:
#> mean sd 10% 50% 90%
#> mean_PPD -25.6 3.1 -29.6 -25.6 -21.6
#>
#> The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).
#>
#> MCMC diagnostics
#> mcse Rhat n_eff
#> (Intercept) 0.1 1.0 952
#> s(times).1 6.4 1.0 1360
#> s(times).2 7.4 1.0 1224
#> s(times).3 4.4 1.0 1217
#> s(times).4 4.1 1.0 1171
#> s(times).5 2.4 1.0 1229
#> s(times).6 1.5 1.0 1088
#> s(times).7 1.1 1.0 1072
#> s(times).8 3.3 1.0 1076
#> s(times).9 1.0 1.0 1178
#> sigma 0.1 1.0 1006
#> smooth_sd[s(times)1] 1.7 1.0 1255
#> smooth_sd[s(times)2] 0.7 1.0 1191
#> mean_PPD 0.1 1.0 1301
#> log-posterior 0.1 1.0 1071
#>
#> For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).LOO 值
#>
#> Computed from 1200 by 133 log-likelihood matrix
#>
#> Estimate SE
#> elpd_loo -611.4 8.7
#> p_loo 7.3 1.3
#> looic 1222.7 17.5
#> ------
#> Monte Carlo SE of elpd_loo is 0.1.
#>
#> Pareto k diagnostic values:
#> Count Pct. Min. n_eff
#> (-Inf, 0.5] (good) 132 99.2% 533
#> (0.5, 0.7] (ok) 1 0.8% 260
#> (0.7, 1] (bad) 0 0.0% <NA>
#> (1, Inf) (very bad) 0 0.0% <NA>
#>
#> All Pareto k estimates are ok (k < 0.7).
#> See help('pareto-k-diagnostic') for details.37.1.4 brms
另一个综合型的贝叶斯分析扩展包是 brms 包
# 拟合模型
mcycle_brms <- brms::brm(accel ~ s(times),
data = mcycle, family = gaussian(), cores = 2, seed = 20232023,
iter = 4000, warmup = 1000, thin = 10, refresh = 0, silent = 2,
control = list(adapt_delta = 0.99)
)
# 模型输出
summary(mcycle_brms)#> Family: gaussian
#> Links: mu = identity; sigma = identity
#> Formula: accel ~ s(times)
#> Data: mcycle (Number of observations: 133)
#> Draws: 4 chains, each with iter = 4000; warmup = 1000; thin = 10;
#> total post-warmup draws = 1200
#>
#> Smooth Terms:
#> Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> sds(stimes_1) 716.18 173.55 447.43 1129.05 1.00 1208 1112
#>
#> Population-Level Effects:
#> Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> Intercept -25.42 1.97 -29.32 -21.52 1.00 1197 1214
#> stimes_1 130.28 282.27 -419.51 704.47 1.00 1070 1173
#>
#> Family Specific Parameters:
#> Estimate Est.Error l-95% CI u-95% CI Rhat Bulk_ESS Tail_ESS
#> sigma 22.73 1.51 19.97 26.01 1.00 1135 1209
#>
#> Draws were sampled using sampling(NUTS). For each parameter, Bulk_ESS
#> and Tail_ESS are effective sample size measures, and Rhat is the potential
#> scale reduction factor on split chains (at convergence, Rhat = 1).固定效应
#> Estimate Est.Error Q2.5 Q97.5
#> Intercept -25.41669 1.972042 -29.32341 -21.51916
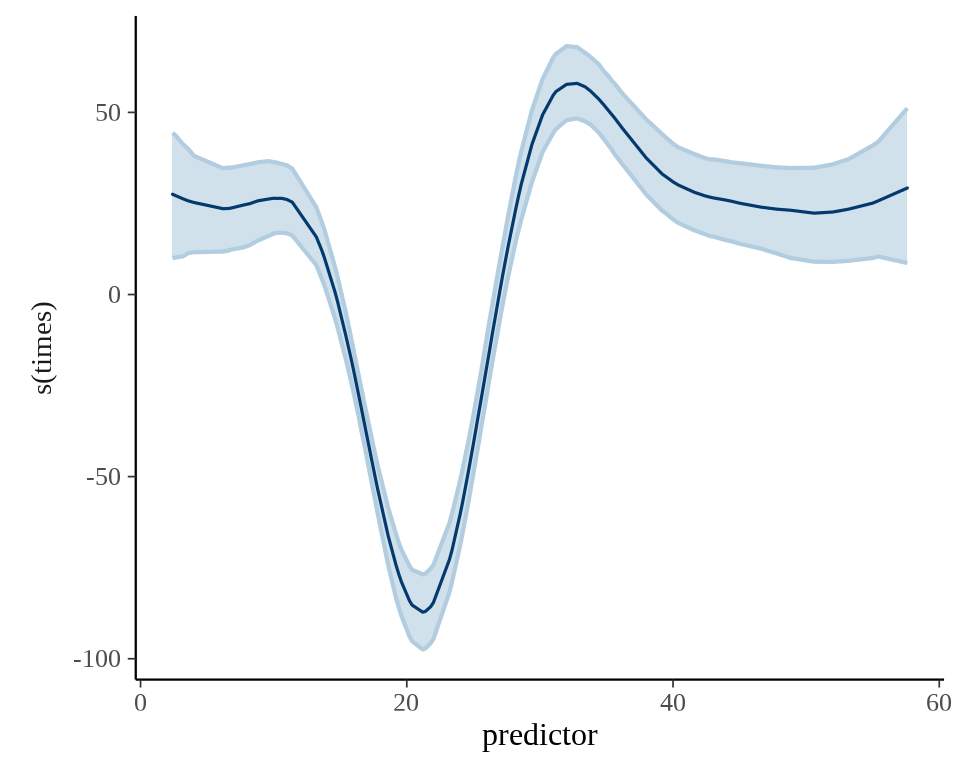
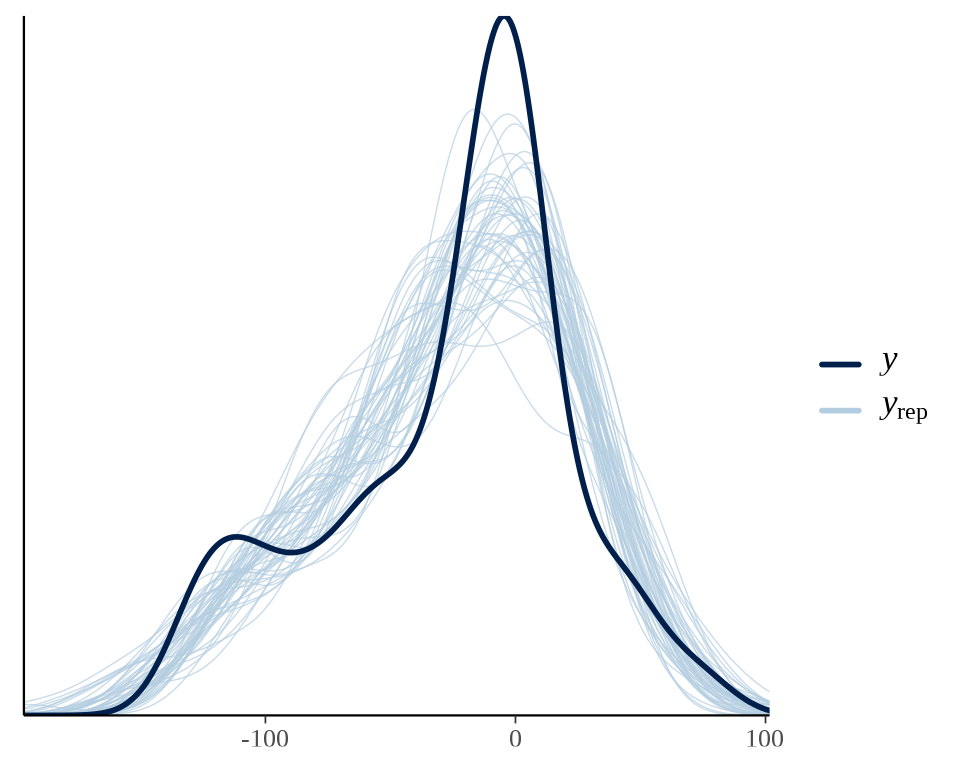
#> stimes_1 130.27592 282.265346 -419.50765 704.46677模型中样条平滑的效应
LOO 值与 rstanarm 包计算的值很接近。
#>
#> Computed from 1200 by 133 log-likelihood matrix
#>
#> Estimate SE
#> elpd_loo -608.6 10.3
#> p_loo 9.1 1.6
#> looic 1217.2 20.5
#> ------
#> Monte Carlo SE of elpd_loo is 0.1.
#>
#> All Pareto k estimates are good (k < 0.5).
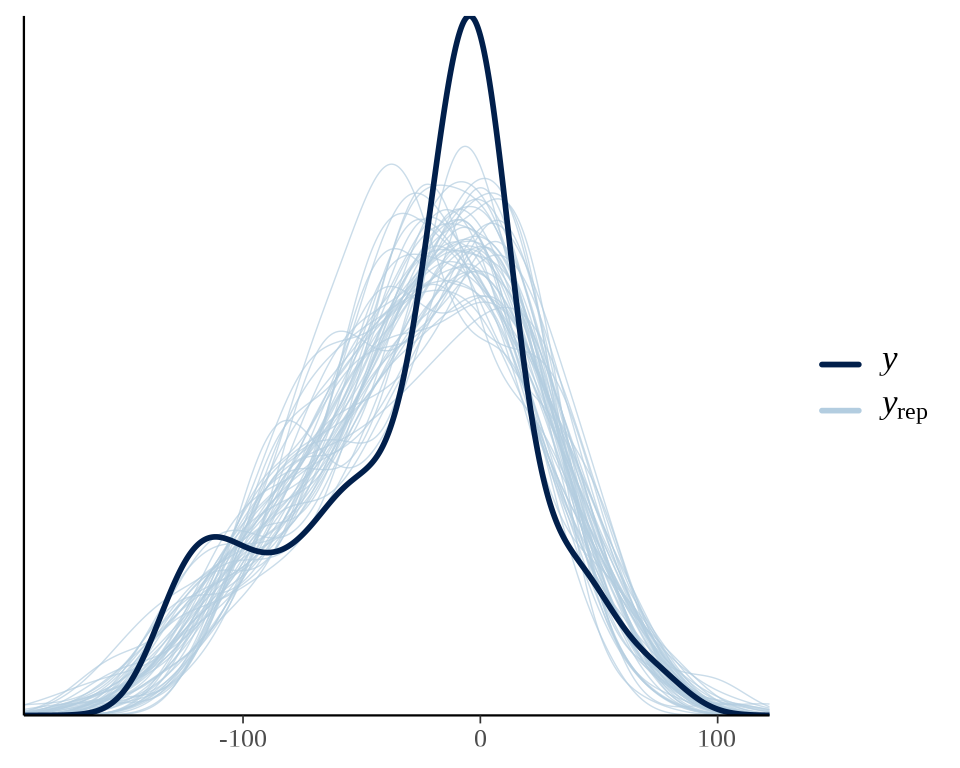
#> See help('pareto-k-diagnostic') for details.后验预测分布检查
37.1.5 GINLA
library(mgcv)
mcycle_mgcv <- gam(accel ~ s(times), data = mcycle, fit = FALSE)
# 简化版 INLA
mcycle_ginla <- ginla(G = mcycle_mgcv)
str(mcycle_ginla)#> List of 2
#> $ density: num [1:10, 1:100] 2.04e-04 2.13e-05 8.21e-06 3.47e-05 1.14e-05 ...
#> $ beta : num [1:10, 1:100] -32.8 -133.4 -139.4 -152.5 -153.3 ...最大后验估计
37.1.6 INLA
37.2 案例:朗格拉普岛核污染
从线性到可加,意味着从线性到非线性,可加模型容纳非线性的成分,比如高斯过程、样条。
37.2.1 mgcv
本节复用 章节 28 朗格拉普岛核污染数据,相关背景不再赘述,下面首先加载数据到 R 环境。
接着,将岛上各采样点的辐射强度展示出来,算是简单回顾一下数据概况。
代码
library(plot3D)
with(rongelap, {
opar <- par(mar = c(.1, 2.5, .1, .1), no.readonly = TRUE)
rongelap_coastline$cZ <- 0
scatter3D(
x = cX, y = cY, z = counts / time,
xlim = c(-6500, 50), ylim = c(-3800, 110),
xlab = "\n横坐标(米)", ylab = "\n纵坐标(米)",
zlab = "\n辐射强度", lwd = 0.5, cex = 0.8,
pch = 16, type = "h", ticktype = "detailed",
phi = 40, theta = -30, r = 50, d = 1,
expand = 0.5, box = TRUE, bty = "b",
colkey = F, col = "black",
panel.first = function(trans) {
XY <- trans3D(
x = rongelap_coastline$cX,
y = rongelap_coastline$cY,
z = rongelap_coastline$cZ,
pmat = trans
)
lines(XY, col = "gray50", lwd = 2)
}
)
rongelap_coastline$cZ <- NULL
on.exit(par(opar), add = TRUE)
})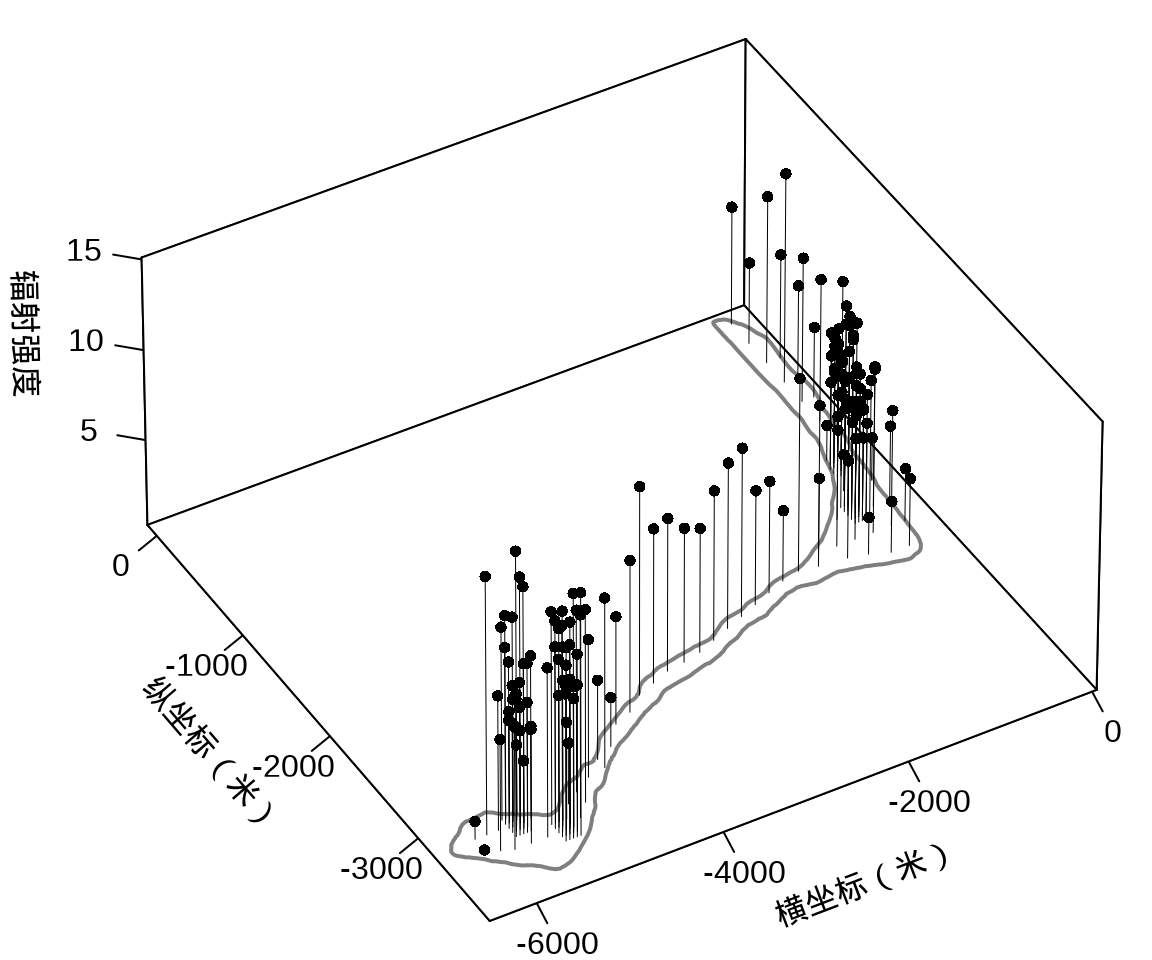
在这里,从广义可加混合效应模型的角度来对核污染数据建模,空间效应仍然是用高斯过程来表示,响应变量服从带漂移项的泊松分布。采用 mgcv 包 (S. N. Wood 2004) 的函数 gam() 拟合模型,其中,含 49 个参数的样条近似高斯过程,高斯过程的核函数为默认的梅隆型。更多详情见 mgcv 包的函数 s() 帮助文档参数的说明,默认值是梅隆型相关函数及默认的范围参数,作者自己定义了一套符号约定。
library(nlme)
library(mgcv)
fit_rongelap_gam <- gam(
counts ~ s(cX, cY, bs = "gp", k = 50), offset = log(time),
data = rongelap, family = poisson(link = "log")
)
# 模型输出
summary(fit_rongelap_gam)#>
#> Family: poisson
#> Link function: log
#>
#> Formula:
#> counts ~ s(cX, cY, bs = "gp", k = 50)
#>
#> Parametric coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 1.976815 0.001642 1204 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Approximate significance of smooth terms:
#> edf Ref.df Chi.sq p-value
#> s(cX,cY) 48.98 49 34030 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> R-sq.(adj) = 0.876 Deviance explained = 60.7%
#> UBRE = 153.78 Scale est. = 1 n = 157#> s(cX,cY)
#> 2543.376值得一提的是核函数的类型和默认参数的选择,参数 m 接受一个向量, m[1] 取值为 1 至 5,分别代表球型 spherical, 幂指数 power exponential 和梅隆型 Matern with \(\kappa\) = 1.5, 2.5 or 3.5 等 5 种相关/核函数。
接下来,基于岛屿的海岸线数据划分出网格,将格点作为新的预测位置。
#> Linking to GEOS 3.12.0, GDAL 3.7.3, PROJ 9.2.1; sf_use_s2() is TRUElibrary(abind)
library(stars)
# 类型转化
rongelap_sf <- st_as_sf(rongelap, coords = c("cX", "cY"), dim = "XY")
rongelap_coastline_sf <- st_as_sf(rongelap_coastline, coords = c("cX", "cY"), dim = "XY")
rongelap_coastline_sfp <- st_cast(st_combine(st_geometry(rongelap_coastline_sf)), "POLYGON")
# 添加缓冲区
rongelap_coastline_buffer <- st_buffer(rongelap_coastline_sfp, dist = 50)
# 构造带边界约束的网格
rongelap_coastline_grid <- st_make_grid(rongelap_coastline_buffer, n = c(150, 75))
# 将 sfc 类型转化为 sf 类型
rongelap_coastline_grid <- st_as_sf(rongelap_coastline_grid)
rongelap_coastline_buffer <- st_as_sf(rongelap_coastline_buffer)
rongelap_grid <- rongelap_coastline_grid[rongelap_coastline_buffer, op = st_intersects]
# 计算网格中心点坐标
rongelap_grid_centroid <- st_centroid(rongelap_grid)
# 共计 1612 个预测点
rongelap_grid_df <- as.data.frame(st_coordinates(rongelap_grid_centroid))
colnames(rongelap_grid_df) <- c("cX", "cY")模型对象 fit_rongelap_gam 在新的格点上预测核辐射强度,接着整理预测结果数据。
# 预测
rongelap_grid_df$ypred <- as.vector(predict(fit_rongelap_gam, newdata = rongelap_grid_df, type = "response"))
# 整理预测数据
rongelap_grid_sf <- st_as_sf(rongelap_grid_df, coords = c("cX", "cY"), dim = "XY")
rongelap_grid_stars <- st_rasterize(rongelap_grid_sf, nx = 150, ny = 75)
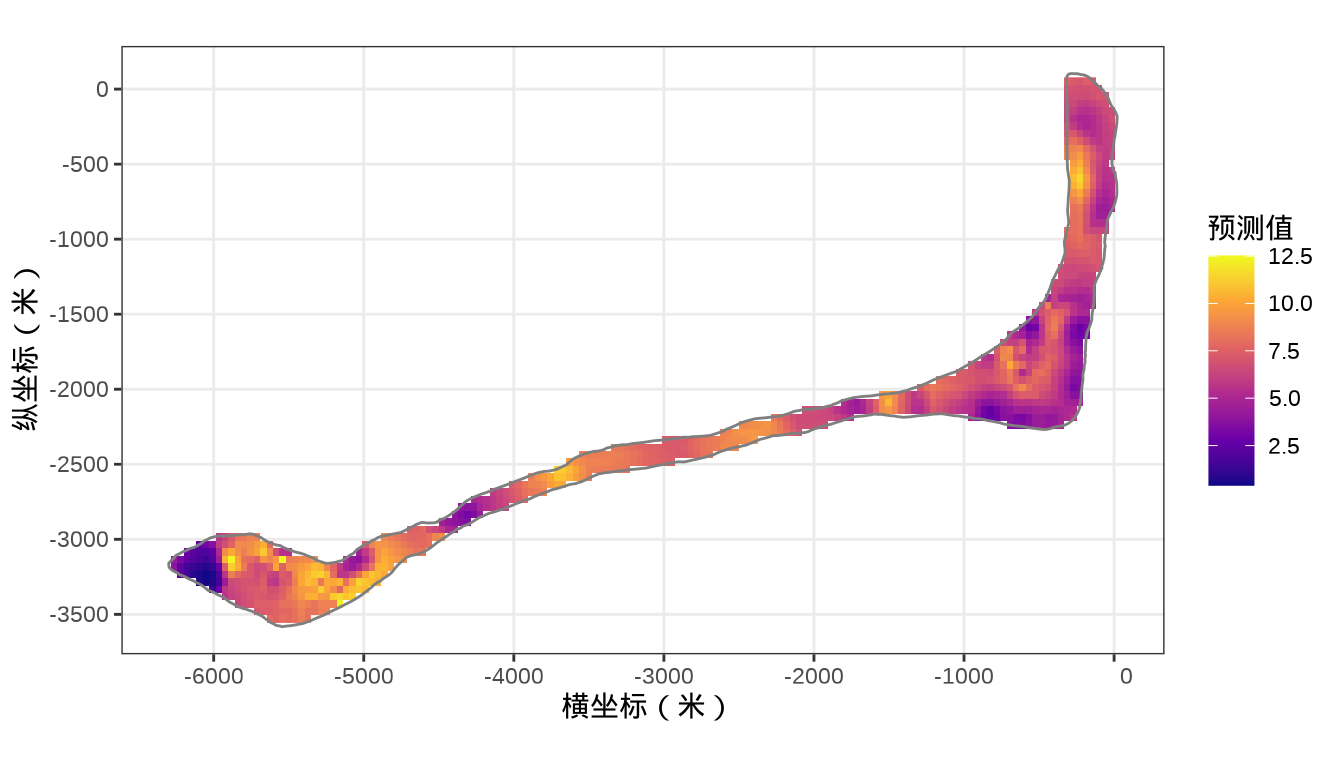
rongelap_stars <- st_crop(x = rongelap_grid_stars, y = rongelap_coastline_sfp)最后,将岛上各个格点的核辐射强度绘制出来,给出全岛核辐射强度的空间分布。
代码
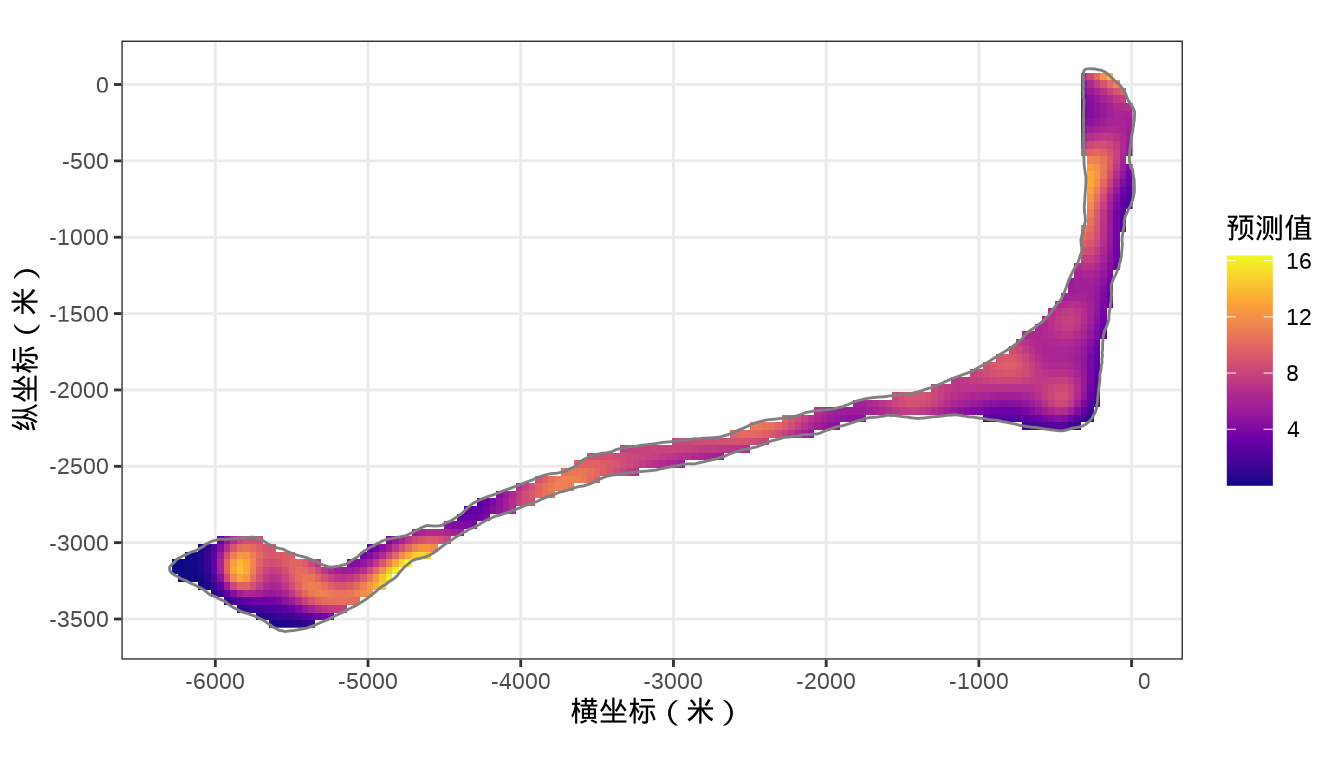
37.2.2 cmdstanr
FRK 包 (Sainsbury-Dale, Zammit-Mangion, 和 Cressie 2022)(Fixed Rank Kriging,固定秩克里金) 可对有一定规模的(时空)空间区域数据和点参考数据集建模,响应变量的分布从高斯分布扩展到指数族,放在(时空)空间广义线性混合效应模型的框架下统一建模。然而,不支持带漂移项的泊松分布。
brms 包支持一大类贝叶斯统计模型,但是对高斯过程建模十分低效,当遇到有一定规模的数据,建模是不可行的,因为经过对 brms 包生成的模型代码的分析,发现它采用潜变量高斯过程(latent variable GP)模型,这也是采样效率低下的一个关键因素。
当设置 \(k = 5\) 时,用 5 个基函数来近似高斯过程,编译完成后,采样速度很快,但是结果不可靠,采样过程中的问题很多,见下文。当将横、纵坐标值同时缩小 6000 倍,采样效率并未得到改善。当设置 \(k = 15\) 时,运行时间明显增加,采样过程的诊断结果类似 \(k = 5\) 的情况,还是不可靠。说明 brms 包不适合处理含高斯过程的模型。
实际上,Stan 没有现成的有效算法或扩展包做有规模的高斯过程建模,详见 Bob Carpenter 在 2023 年 Stan 大会的报告,因此,必须采用一些近似方法,通过 Stan 编码实现。接下来,分别手动实现低秩和基样条两种方法近似边际高斯过程(marginal likelihood GP)(Rasmussen 和 Williams 2006),用 Stan 编码模型。代码文件分别是 rongelap_poisson_lr.stan 和 rongelap_poisson_splines.stan 。
37.2.3 GINLA
mgcv 包的函数 ginla() 实现简化版的 Integrated Nested Laplace Approximation, INLA (Simon N. Wood 2019)。
rongelap_gam <- gam(
counts ~ s(cX, cY, bs = "gp", k = 50), offset = log(time),
data = rongelap, family = poisson(link = "log"), fit = FALSE
)
# 简化版 INLA
rongelap_ginla <- ginla(G = rongelap_gam)
str(rongelap_ginla)#> List of 2
#> $ density: num [1:50, 1:100] 2.49e-01 9.03e-06 3.51e-06 1.97e-06 1.17e-06 ...
#> $ beta : num [1:50, 1:100] 1.97 -676.61 -572.67 4720.77 240.12 ...其中, \(k = 50\) 表示 49 个样条参数,每个参数的分布对应有 100 个采样点,另外,截距项的边际后验概率密度分布如下:
plot(
rongelap_ginla$beta[1, ], rongelap_ginla$density[1, ],
type = "l", xlab = "截距项", ylab = "概率密度"
)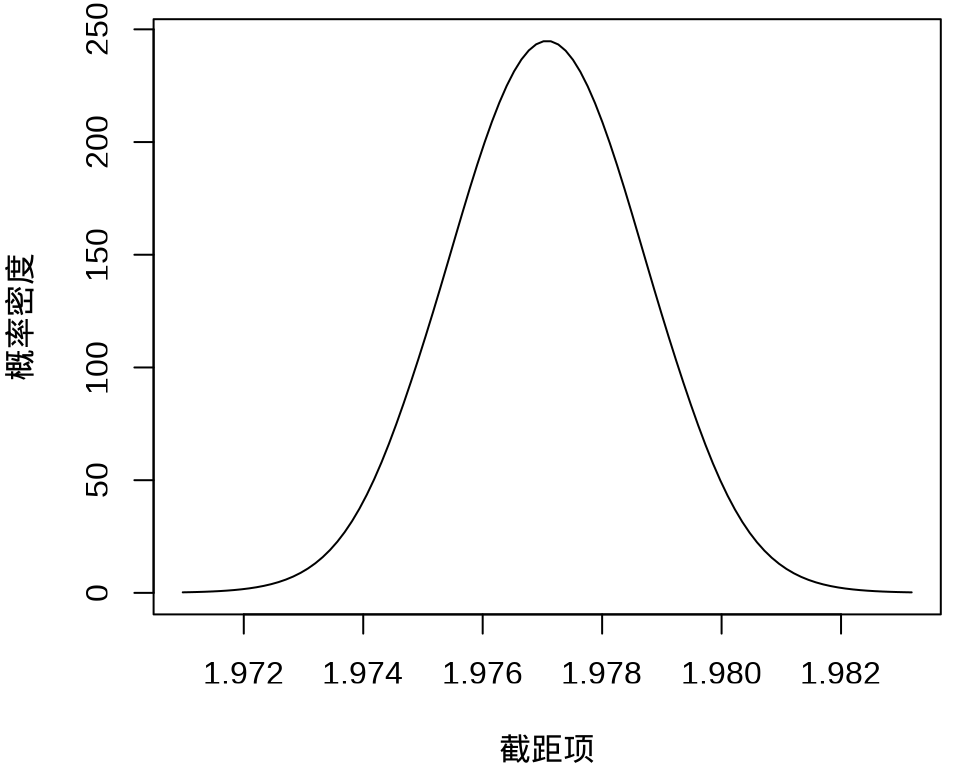
不难看出,截距项在 1.976 至 1.978 之间,50个参数的最大后验估计分别如下:
#> [1] 1.977019e+00 -5.124099e+02 5.461183e+03 1.515296e+03 -2.822166e+03
#> [6] -1.598371e+04 -6.417855e+03 1.938122e+02 -4.270878e+03 3.769951e+03
#> [11] -1.002035e+04 1.914717e+03 -9.721572e+03 -3.794461e+04 -1.401549e+04
#> [16] -5.376582e+04 -1.585899e+04 -2.338235e+04 6.239053e+04 -3.574500e+02
#> [21] -4.587927e+04 1.723604e+04 -4.514781e+03 9.184026e-02 3.496526e-01
#> [26] -1.477406e+02 4.585057e+03 9.153647e+03 1.929387e+04 -1.116512e+04
#> [31] -1.166149e+04 8.079451e+02 3.627369e+03 -9.835680e+03 1.357777e+04
#> [36] 1.487742e+04 3.880562e+04 -1.708858e+03 2.775844e+04 2.527415e+04
#> [41] -3.932957e+04 3.548123e+04 -1.116341e+04 1.630910e+04 -9.789381e+02
#> [46] -2.011250e+04 2.699657e+04 -4.744393e+04 2.753347e+04 2.834356e+0437.2.4 INLA
接下来,介绍完整版的近似贝叶斯推断方法 INLA — 集成嵌套拉普拉斯近似 (Integrated Nested Laplace Approximations,简称 INLA) (Rue, Martino, 和 Chopin 2009)。根据研究区域的边界构造非凸的内外边界,处理边界效应。
library(INLA)
library(splancs)
# 构造非凸的边界
boundary <- list(
inla.nonconvex.hull(
points = as.matrix(rongelap_coastline[,c("cX", "cY")]),
convex = 100, concave = 150, resolution = 100),
inla.nonconvex.hull(
points = as.matrix(rongelap_coastline[,c("cX", "cY")]),
convex = 200, concave = 200, resolution = 200)
)根据研究区域的情况构造网格,边界内部三角网格最大边长为 300,边界外部最大边长为 600,边界外凸出距离为 100 米。
构建 SPDE,指定自协方差函数为指数型,则 \(\nu = 1/2\) ,因是二维平面,则 \(d = 2\) ,根据 \(\alpha = \nu + d/2\) ,从而 alpha = 3/2 。
生成 SPDE 模型的指标集,也是随机效应部分。
#> s s.group s.repl
#> 691 691 691投影矩阵,三角网格和采样点坐标之间的投影。观测数据 rongelap 和未采样待预测的位置数据 rongelap_grid_df
# 观测位置投影到三角网格上
A <- inla.spde.make.A(mesh = mesh, loc = as.matrix(rongelap[, c("cX", "cY")]) )
# 预测位置投影到三角网格上
coop <- as.matrix(rongelap_grid_df[, c("cX", "cY")])
Ap <- inla.spde.make.A(mesh = mesh, loc = coop)
# 1612 个预测位置
dim(Ap)#> [1] 1612 691准备观测数据和预测位置,构造一个 INLA 可以使用的数据栈 Data Stack。
# 在采样点的位置上估计 estimation stk.e
stk.e <- inla.stack(
tag = "est",
data = list(y = rongelap$counts, E = rongelap$time),
A = list(rep(1, 157), A),
effects = list(data.frame(b0 = 1), s = indexs)
)
# 在新生成的位置上预测 prediction stk.p
stk.p <- inla.stack(
tag = "pred",
data = list(y = NA, E = NA),
A = list(rep(1, 1612), Ap),
effects = list(data.frame(b0 = 1), s = indexs)
)
# 合并数据 stk.full has stk.e and stk.p
stk.full <- inla.stack(stk.e, stk.p)指定响应变量与漂移项、联系函数、模型公式。
# 精简输出
inla.setOption(short.summary = TRUE)
# 模型拟合
res <- inla(formula = y ~ 0 + b0 + f(s, model = spde),
data = inla.stack.data(stk.full),
E = E, # E 已知漂移项
control.family = list(link = "log"),
control.predictor = list(
compute = TRUE,
link = 1, # 与 control.family 联系函数相同
A = inla.stack.A(stk.full)
),
control.compute = list(
cpo = TRUE,
waic = TRUE, # WAIC 统计量 通用信息准则
dic = TRUE # DIC 统计量 偏差信息准则
),
family = "poisson"
)
# 模型输出
summary(res)#> Fixed effects:
#> mean sd 0.025quant 0.5quant 0.975quant mode kld
#> b0 1.828 0.061 1.706 1.828 1.948 1.828 0
#>
#> Model hyperparameters:
#> mean sd 0.025quant 0.5quant 0.975quant mode
#> Theta1 for s 2.00 0.062 1.88 2.00 2.12 2.00
#> Theta2 for s -4.85 0.130 -5.11 -4.85 -4.59 -4.85
#>
#> Deviance Information Criterion (DIC) ...............: 1834.57
#> Deviance Information Criterion (DIC, saturated) ....: 314.90
#> Effective number of parameters .....................: 156.46
#>
#> Watanabe-Akaike information criterion (WAIC) ...: 1789.32
#> Effective number of parameters .................: 80.06
#>
#> is computedkld表示 Kullback-Leibler divergence (KLD) 它的值描述标准高斯分布与 Simplified Laplace Approximation 之间的差别,值越小越表示拉普拉斯的近似效果好。DIC 和 WAIC 指标都是评估模型预测表现的。另外,还有两个量计算出来了,但是没有显示,分别是 CPO 和 PIT 。CPO 表示 Conditional Predictive Ordinate (CPO),PIT 表示 Probability Integral Transforms (PIT) 。
固定效应(截距)和超参数部分
#> mean sd 0.025quant 0.5quant 0.975quant mode kld
#> b0 1.828027 0.06147353 1.706422 1.828284 1.948169 1.828279 1.782546e-08#> mean sd 0.025quant 0.5quant 0.975quant mode
#> Theta1 for s 2.000684 0.06235058 1.876512 2.001169 2.122006 2.003209
#> Theta2 for s -4.851258 0.12973385 -5.105061 -4.851807 -4.594253 -4.854093提取预测数据,并整理数据。
# 预测值对应的指标集合
index <- inla.stack.index(stk.full, tag = "pred")$data
# 提取预测结果,后验均值
# pred_mean <- res$summary.fitted.values[index, "mean"]
# 95% 预测下限
# pred_ll <- res$summary.fitted.values[index, "0.025quant"]
# 95% 预测上限
# pred_ul <- res$summary.fitted.values[index, "0.975quant"]
# 整理数据
rongelap_grid_df$ypred <- res$summary.fitted.values[index, "mean"]
# 预测值数据
rongelap_grid_sf <- st_as_sf(rongelap_grid_df, coords = c("cX", "cY"), dim = "XY")
rongelap_grid_stars <- st_rasterize(rongelap_grid_sf, nx = 150, ny = 75)
rongelap_stars <- st_crop(x = rongelap_grid_stars, y = rongelap_coastline_sfp)最后,类似之前 mgcv 建模的最后一步,将 INLA 的预测结果绘制出来。
37.3 案例:城市土壤重金属污染
介绍多元地统计(Multivariate geostatistics)建模分析与 INLA 实现。分析某城市地表土壤重金属污染情况,找到污染最严重的地方,即寻找重金属污染的源头。
city_data <- readRDS(file = "data/cumcm2011A.rds")
library(sf)
city_data <- st_as_sf(city_data, coords = c("x(m)", "y(m)"), dim = "XY")
city_data#> Simple feature collection with 319 features and 12 fields
#> Geometry type: POINT
#> Dimension: XY
#> Bounding box: xmin: 0 ymin: 0 xmax: 28654 ymax: 18449
#> CRS: NA
#> First 10 features:
#> 编号 功能区 海拔(m) 功能区名称 As (μg/g) Cd (ng/g) Cr (μg/g) Cu (μg/g)
#> 1 1 4 5 交通区 7.84 153.8 44.31 20.56
#> 2 2 4 11 交通区 5.93 146.2 45.05 22.51
#> 3 3 4 28 交通区 4.90 439.2 29.07 64.56
#> 4 4 2 4 工业区 6.56 223.9 40.08 25.17
#> 5 5 4 12 交通区 6.35 525.2 59.35 117.53
#> 6 6 2 6 工业区 14.08 1092.9 67.96 308.61
#> 7 7 4 15 交通区 8.94 269.8 95.83 44.81
#> 8 8 2 7 工业区 9.62 1066.2 285.58 2528.48
#> 9 9 4 22 交通区 7.41 1123.9 88.17 151.64
#> 10 10 4 7 交通区 8.72 267.1 65.56 29.65
#> Hg (ng/g) Ni (μg/g) Pb (μg/g) Zn (μg/g) geometry
#> 1 266 18.2 35.38 72.35 POINT (74 781)
#> 2 86 17.2 36.18 94.59 POINT (1373 731)
#> 3 109 10.6 74.32 218.37 POINT (1321 1791)
#> 4 950 15.4 32.28 117.35 POINT (0 1787)
#> 5 800 20.2 169.96 726.02 POINT (1049 2127)
#> 6 1040 28.2 434.80 966.73 POINT (1647 2728)
#> 7 121 17.8 62.91 166.73 POINT (2883 3617)
#> 8 13500 41.7 381.64 1417.86 POINT (2383 3692)
#> 9 16000 25.8 172.36 926.84 POINT (2708 2295)
#> 10 63 21.7 36.94 100.41 POINT (2933 1767)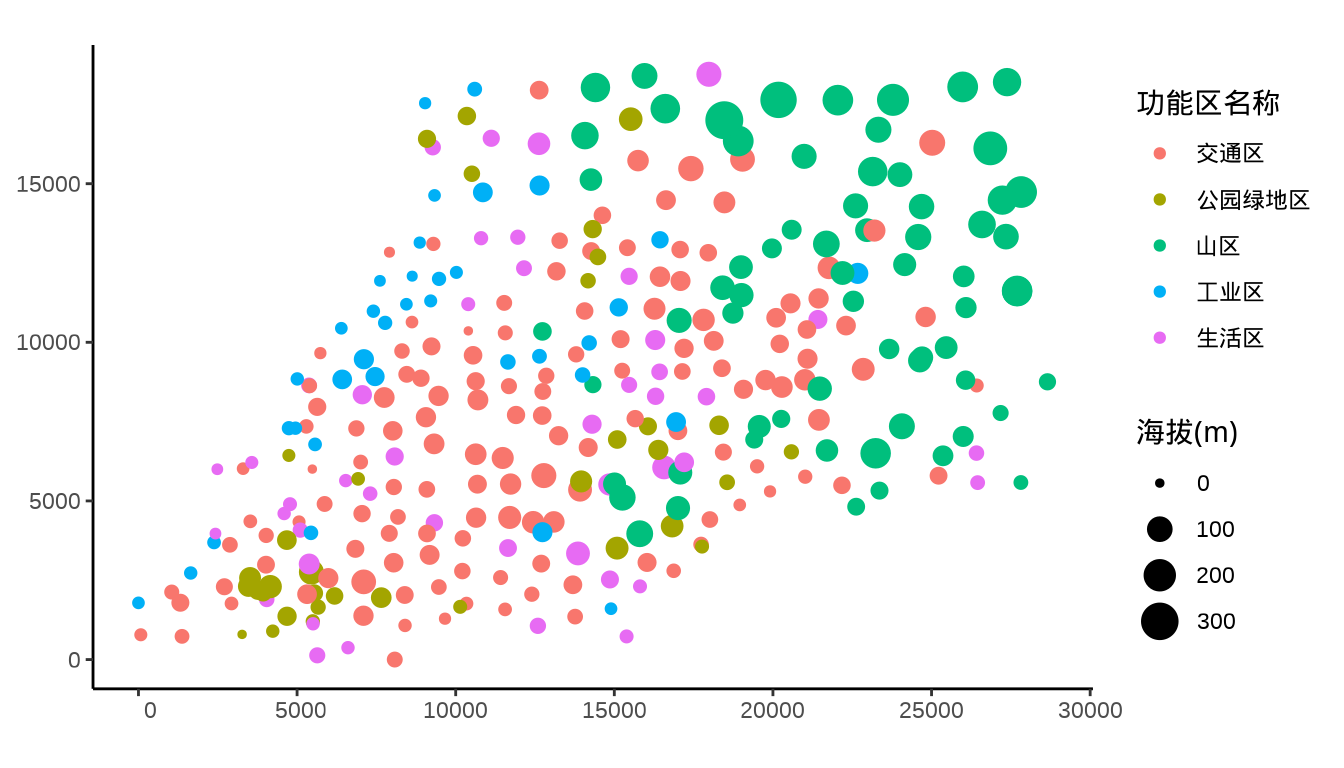
library(ggplot2)
ggplot(data = city_data) +
geom_sf(aes(color = `功能区名称`, size = `As (μg/g)`)) +
theme_classic()
ggplot(data = city_data) +
geom_sf(aes(color = `功能区名称`, size = `Cd (ng/g)`)) +
theme_classic()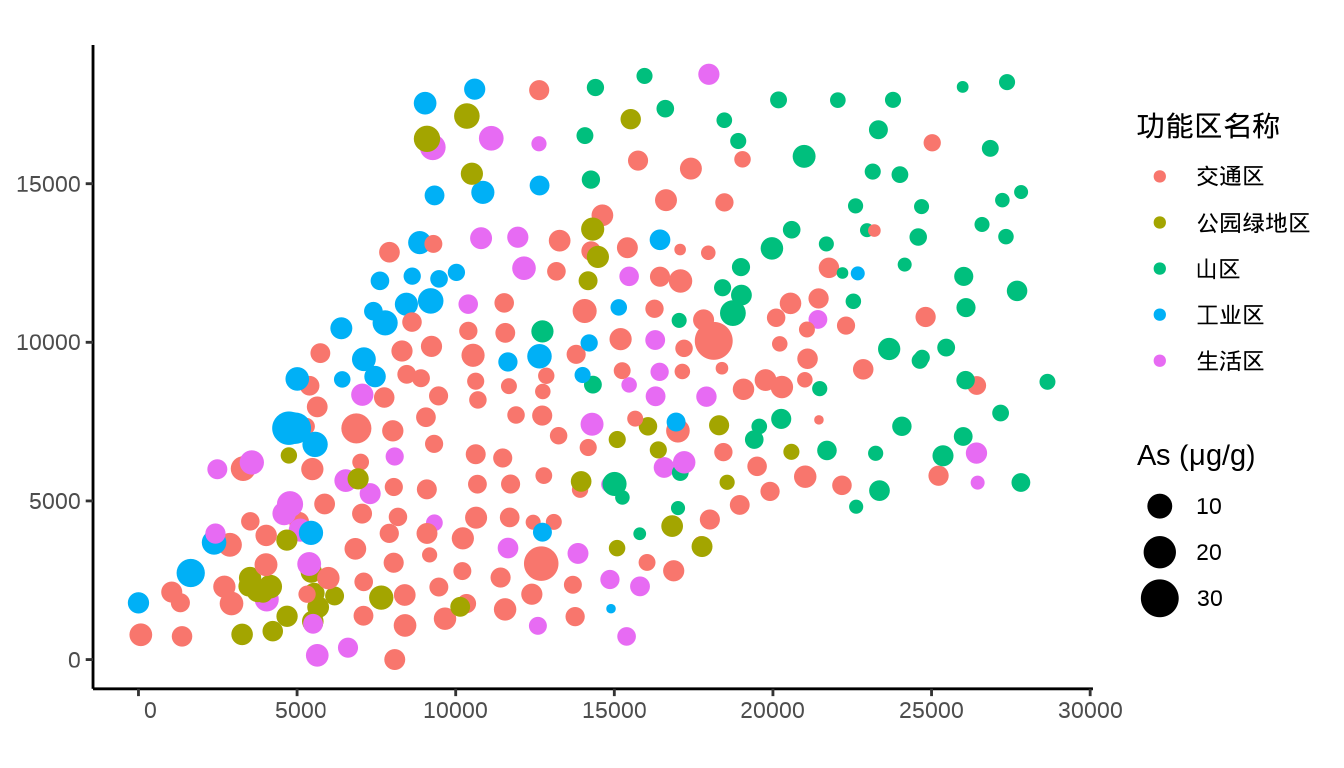
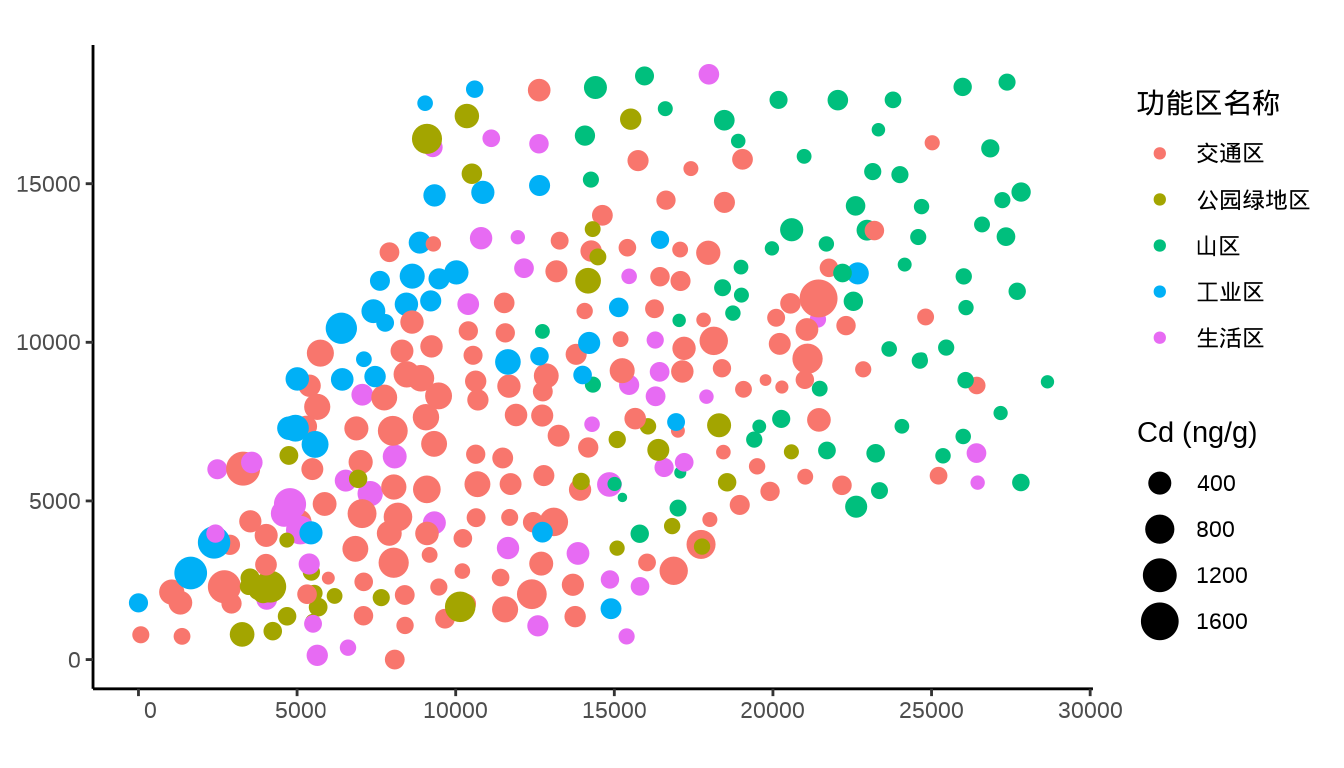
为了便于建模,对数据做标准化处理。
# 根据背景值将各个重金属浓度列进行转化
city_data <- within(city_data, {
`As (μg/g)` <- (`As (μg/g)` - 3.6) / 0.9
`Cd (ng/g)` <- (`Cd (ng/g)` - 130) / 30
`Cr (μg/g)` <- (`Cr (μg/g)` - 31) / 9
`Cu (μg/g)` <- (`Cu (μg/g)` - 13.2) / 3.6
`Hg (ng/g)` <- (`Hg (ng/g)` - 35) / 8
`Ni (μg/g)` <- (`Ni (μg/g)` - 12.3) / 3.8
`Pb (μg/g)` <- (`Pb (μg/g)` - 31) / 6
`Zn (μg/g)` <- (`Zn (μg/g)` - 69) / 14
})当我们逐一检查各个重金属的浓度分布时,发现重金属汞 Hg 在四个地方的浓度极高,暗示着如果数据采集没有问题,那么这几个地方很可能是污染源。
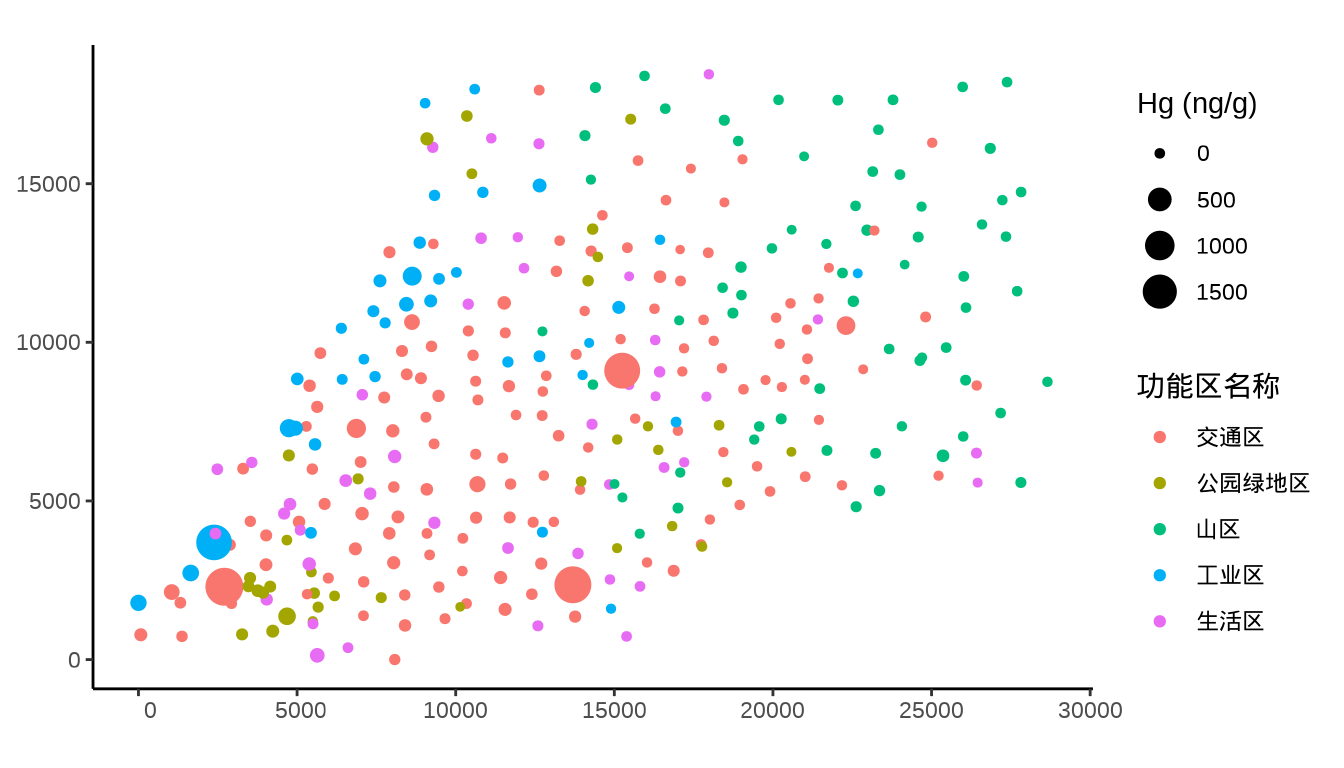
37.3.1 mgcv
mgcv 包用于基于惩罚似然的多元模型平滑参数估计和选择 (Simon N. Wood, Pya, 和 Säfken 2016)。
37.3.2 INLA
INLA 包用于多元空间模型的贝叶斯推断 (Palmí-Perales 等 2022) 。